15. 定常クリープ速度計算ワークフロー¶

15.1. 概要¶

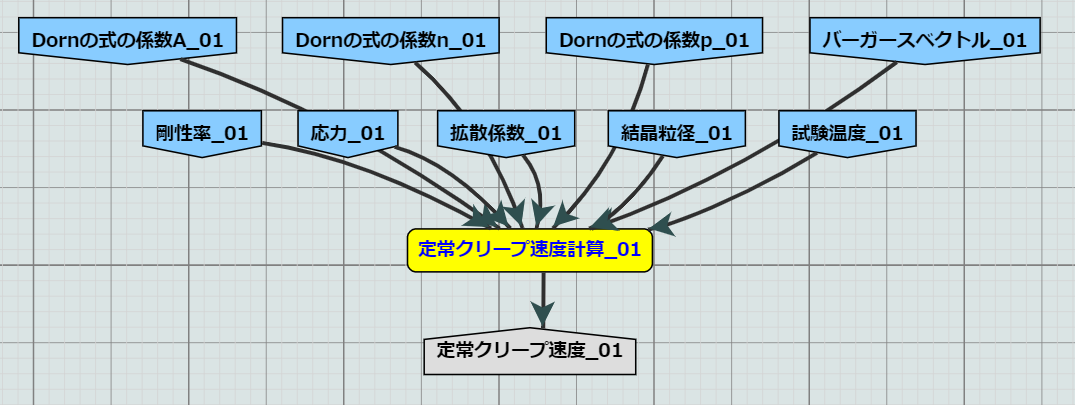
本ワークフローはDornの式により定常クリープ速度を計算するワークフローである。

15.1.1. Dornの式¶

定常クリープ速度の計算には、参考文献 1 の式(1) より引用したDornの式 (10) を利用している。

(10)¶\[\begin{split}& \dot{\epsilon} = \frac{AGb}{kT}D_L(\frac{b}{d})^p(\frac{\sigma}{G})^n\\ & \dot{\epsilon} : 定常クリープ速度[s^{-1}]\\ & D:拡散係数[m^2/s]\\ & k:ボルツマン定数\\ & G:剛性率[GPa]\\ & \sigma：応力[MPa]\\ & T:試験温度[\mathrm{K}]\\ & b:バーガースベクトル[m]\\ & d:結晶粒径[\mu m]\\ & A:Dorn式の係数A\\ & p:Dorn式の係数p\\ & n:Dorn式の係数n\\\end{split}\]

1(1,2): Creep Deformation of Type 2205 Duplex Stainless Steel and its Constituent Phases Heeyong Park, Bruno Charles De Cooman https://www.jstage.jst.go.jp/article/isijinternational/54/4/54_945/_article

15.1.2. Dornの式の各変数¶

Dorn式 (10) の各変数値は温度[K]、応力[MPa]、鋼種の属する相(Ferrite, Austainite, DSS 2 のいずれか)を元に、表 10 表 11 表 12 より求める。具体例についてはワークフロー実行に記載する。これらの表は参考文献 1 のTable2～4より引用した。

2: Duplex Stainless Steel

表 10 Table 2¶
Mechanism	D	n	p
Lattice diffusion creep	\(D_{L}\)	1	2
Grain boundary diffusion creep	\(D_{GB}\)	1	3
Grain Boundary Sliding (Superplasticity)	\(D_{L}/D_{GB}\)	2	1/2
Viscous glide	\(D_{L}\)	3	0
Dislocation climb	\(D_{L}\)	5	0

表 11 Table 3¶
Parameter		Value
Phase	Ferrite	Austenite	Duplex
Lattice diffusion coefficient \(D_{0L}\), \(m^{2}/s\)	\(1.9 \times 10^{-4}\)	\(1.8 \times 10^{-5}\)	\(3.5 \times 10^{-5}\)
Grain boundary diffusion coefficient \(\delta D_{0GB}\), \(m^{3}/s\)	\(1.1 \times 10^{-12}\)	\(7.5 \times 10^{-14}\)	\(1.7 \times 10^{-13}\)
Activation energy for lattice diffusion \(Q_{L}\), kJ/mol	239	\(270\)	\(270\)
Activation energy for grain boundary diffusion \(Q_{GB}\), kJ/mol	174	\(159\)	\(163\)
Grain size D, μm	27.400	\(1.050\)	\(0.836\)
Atomic volume \(\Omega\), \(m^{3}\)	\(1.18 \times 10^{–29}\)	\(1.21 \times 10^{-29}\)	\(1.20 \times 10^{-29}\)
Burger’s vector b, m	\(2.48 \times 10^{–10}\)	\(2.58 \times 10^{-10}\)	\(2.53 \times 10^{-10}\)
Shear modulus G, GPa	\(\frac{250.480−0.103T}{2.925}\)	\(\frac{197.398−0.063T}{2.620}\)	\(\frac{209.7115−0.072T}{2.809}\)
Elastic modulus E, GPa	250.480 – 0.103T	\(197.398 – 0.063T\)	\(209.7115 – 0.072T\)
Poisson ratio \(\nu\)	0.4625	\(0.310\)	\(0.40425\)
Melting temperature \(T_{M}\), K	1769	\(1723\)	\(1733\)

表 12 Table 4¶
Phase	D	n	p	A	Mechanism	Stress range at 1323 K
Ferrite	\(D_{L}\)	1	2	32.49	Lattice diffusion creep	< 2.37 MPa
	\(D_{L}\)	3	0	0.73	Viscous glide	> 2.37 MPa
Austenite	\(D_{L}\)	1	2	29.59	Lattice diffusion creep	< 26.4 MPa
	\(D_{L}\)	5	0	\(5 \times 10^{5}\)	Dislocation climb	> 26.4 MPa
DSS	\(D_{L}\)	1	2	31.12	Lattice diffusion creep	< 2.86 MPa
	\(D_{L}\)	2	1	\(1.17 \times 10^{10}T/E\)	Grain Boundary Sliding (Superplasticity)	> 2.86 MPa

表 10 の \(D_{L}\) \(D_{GB}\) はそれぞれ以下の式 (11) 式 (12) から求められる。

(11)¶\[D_{L} = D_{0L}\exp(-Q_{L}/RT)\]

(12)¶\[\begin{split}D_{GB} = D_{0GB}\exp(-Q_{GB}/RT)\\ R:気体定数 \: 8.31446262 \: m^{2} \: kg \: s^{-2} \: K^{-1} \: mol^{−1}\end{split}\]

15.2. ワークフローの説明¶

15.2.1. ワークフロー¶

Dorn式の各変数から定常クリープ速度を予測する。ワークフローは図 154 の通りである。

図 154 定常クリープ速度計算ワークフロー¶

15.2.2. ツール¶

このワークフローは「定常クリープ速度計算」ツールのみで構成されるため、ワークフローとツールの入出力は同一である。

定常クリープ速度計算
定常クリープ速度を予測する。図は図 154 同様である。
- 入力ポート
  ポート名：応力
  任意の応力。単位は[MPa]
  
  10
  
  ポート名: 試験温度
  任意の試験温度。単位は[K]。
  
  1323
  
  ポート名：Dorn式の係数A
  Dorn式の係数A、表 12 より温度1323[K]のときの応力と相から決定する。
  
  29.59
  
  ポート名：Dorn式の係数n
  Dorn式の係数n、表 12 より温度1323[K]のときの応力と相から決定する。
  
  1
  
  ポート名：Dorn式の係数p
  Dorn式の係数p、表 12 より温度1323[K]のときの応力と相から決定する。
  
  2
  
  ポート名：バーガースベクトル
  バーガースベクトル。表 11 のパラメータ Burger's vector より、相に応じて決定する。
  
  2.58e-10
  
  ポート名：剛性率
  剛性率。表 11 のパラメータ Shear modulus より、相に応じて決定する。
  
  43.5301
  
  ポート名：拡散係数
  拡散係数。
  
  3.9386e-16
  
  ポート名：結晶粒径
  結晶粒径。表 11 のパラメータ Grain size より、相に応じて決定する。
- 出力ポート
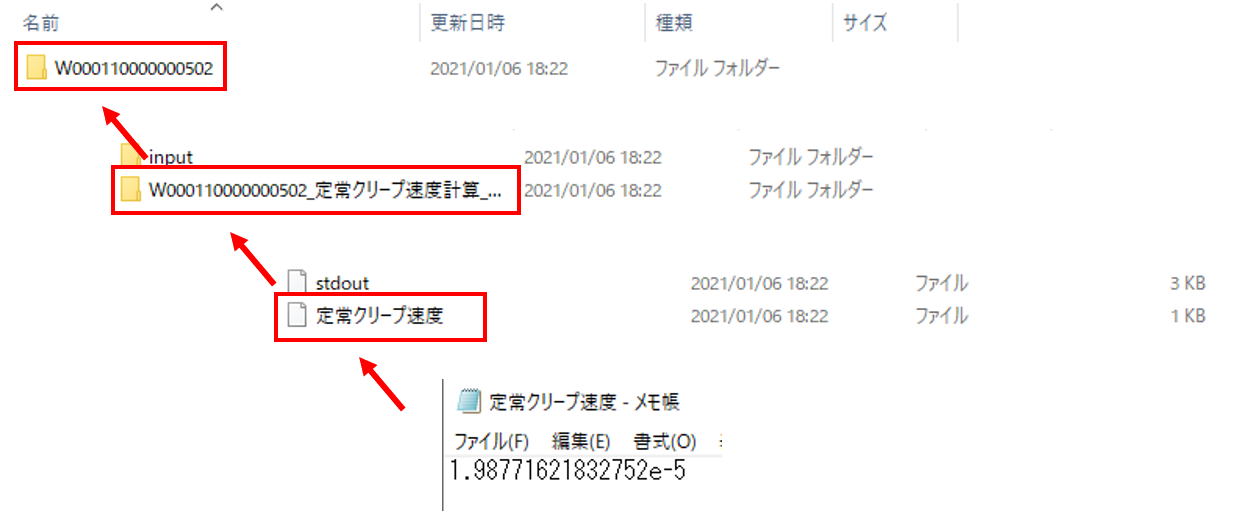
  ポート名:定常クリープ速度
  定常クリープ速度。単位は \(s^{-1}\) 。
  
  0.0000993876

15.2.3. 入力ファイル¶

このワークフローの入力ファイルはツールに示す入力ポートのファイル全てである。入力ファイルはテキストエディタなどで作成する。具体的な作成例をワークフロー実行に示す。サンプル入出力ファイル ダウンロードはこちら （html版のみダウンロード可能）

15.3. ワークフロー実行¶

15.3.1. 前提条件の設定と変数の値の決定¶

本例では前提条件を表 13 のように定め、表 10 表 11 表 12 より変数の値を決定する。

表 13 前提条件一覧¶
条件	値	単位
温度	1323	K
応力	2	MPa
相	Ferrite

拡散係数の計算式、 Dorn式の係数n、p、A
表 13 より、相は"Ferrite" で温度条件が1323[K]のとき応力が2[MPa]である。該当する拡散係数、Dorn式の係数n、p、Aの値を表 12 より決定する。

表 14 拡散係数の計算式、 Dorn式の係数n、p、Aの値¶

変数

値

拡散係数の計算式

\(D_{L}\)

Dorn式の係数n

1

Dorn式の係数p

2

Dorn式の係数A

32.49
バーガースベクトル、剛性率、結晶粒径
表 13 より、相は"Ferrite" であるから表 11 よりFerrite相の、 Burger's vector(バーガースベクトル)、Shear modulus(剛性率)、Grain size(結晶粒径)をそれぞれ決定する。

表 15 バーガースベクトル、剛性率、結晶粒径¶

変数

値

バーガースベクトル

2.48e-10

剛性率

39.0464

結晶粒径

27.4e-6
拡散係数の決定
1. 計算式の決定
  表 14 より \(D = D_{L}\) である。 \(D_{L}\) は式 (11) によって求められる。
2. 拡散係数の計算
  式 (11) の変数に値を代入し、拡散係数を計算する。表 13 より、相は"Ferrite" であるから表 11 より \(D_{0L}\) \(Q_{L}\) はそれぞれ、 \(1.9 \times 10^{-4} m^{2}/s\) 、239 kJ/mol と決定される。気体定数は \(8.31446262 \: m^{2} \: kg \: s^{-2} \: K^{-1} \: mol^{−1}\) 、温度は表 13 より、1323Kとして、それぞれ代入する。
  
  \[\begin{split}D_{L} &= 1.9 \times 10^{-4} \exp( -239 \times 10^{3} / 8.31446262 \times 1323) \\ &=6.96223e-14\end{split}\]
  
  表 16 拡散係数¶
  
  変数
  
  値
  
  拡散係数
  
  6.96223e-14

以上で、ワークフロー実行に必要な値が揃った。

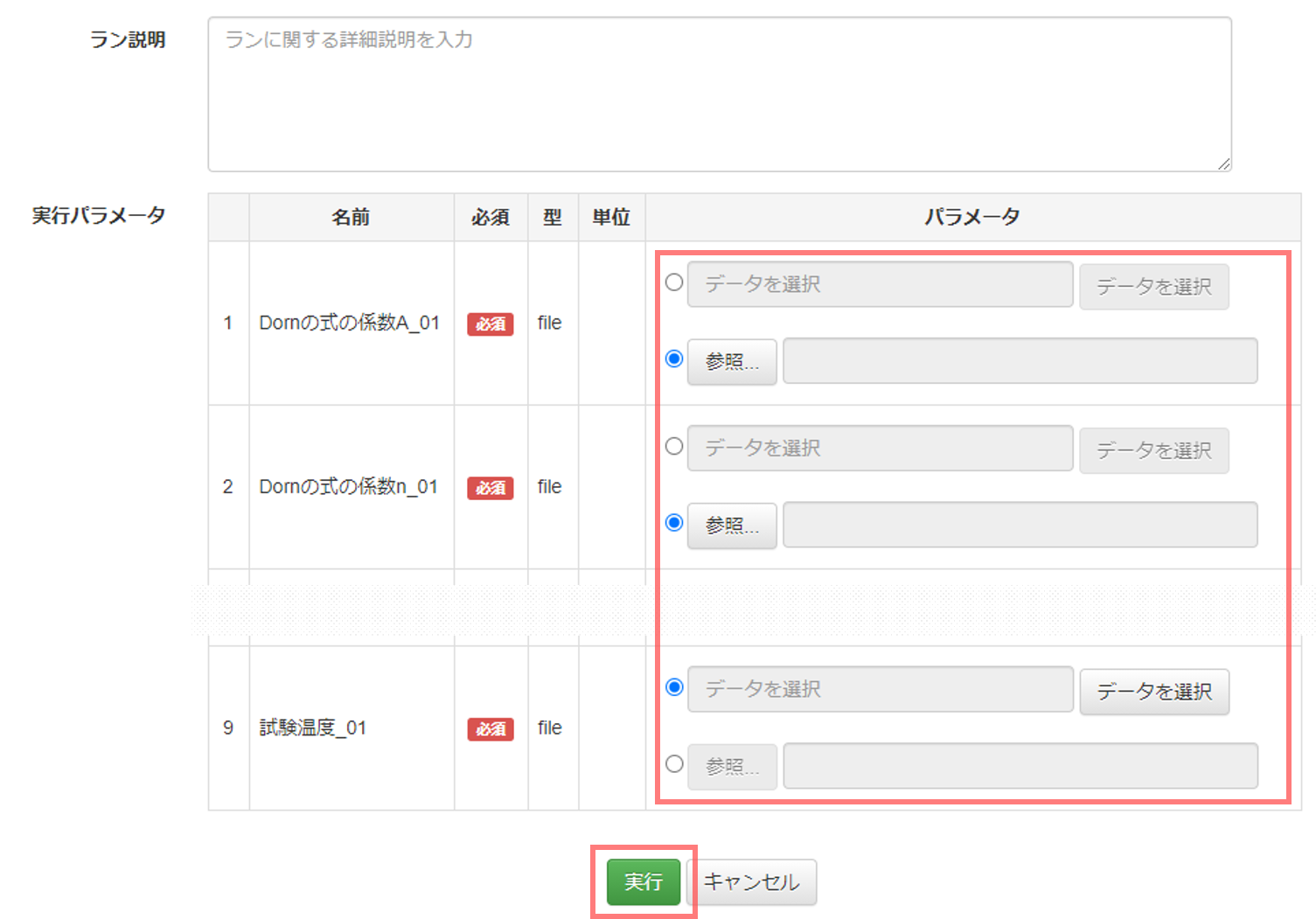
15.3.2. 入力ファイルの作成¶

入力ファイルはテキストエディタなどで作成する。以下にDorn式の係数Aの入力ファイルを作成する例を示す。

Windowsのメモ帳を開く(エディタなら何でもよい)
入力値を記述
ここでは前提条件の設定と変数の値の決定で決定したDorn式の係数A="32.49"を入力

図 155 メモ帳での入力ファイル作成例¶
ファイルを保存
ファイル名は任意。ただし半角スペースを使用してはならない。
前提条件の設定と変数の値の決定で決定した変数の値それぞれについて、1~3の手順でファイルを作成する。

15.3.3. 実行方法¶

ワークフローに入力ファイルの作成で作成した入力ファイルを投入し、定常クリープ速度の計算結果を取得する。

ワークフロー一覧画面( 図 156 )でワークフロー名 [定常クリープ速度] リンクをクリックして、ワークフローメタ情報画面に遷移する。

図 156 ワークフロー一覧画面¶

ワークフローメタ情報画面で、画面の右上にある [ワークフローを実行] ボタンをクリックするとワークフロー実行画面に遷移する( 図 157 )。
実行パラメータ(入力ファイル)を設定後、[実行] ボタンをクリックすることでワークフローが実行される。( 図 158 )

図 157 ワークフローメタ情報画面¶

図 158 ワークフロー実行画面¶

ワークフローが実行されるとラン一覧に実行したワークフローが表示される。( 図 159 )
ランの実行が正常終了すると実行結果のダウンロードが可能になる。

図 159 ラン一覧画面（実行完了）¶

15.3.4. 実行結果の確認方法¶

実行結果をダウンロードする。

ラン一覧から実行結果をダウンロードしたいランIDをクリックし、ラン詳細画面に遷移する( 図 160 )。
ラン詳細画面の [ダウンロード] ボタンをクリックすると計算結果ファイルダウンロードダイアログに遷移する( 図 161 )。

図 160 ラン詳細画面¶
計算結果ファイルダウンロードダイアログの [全ての実行結果をダウンロードする]ラジオボタンをチェックし、[ダウンロードする] ボタンをクリックする。
ダウンロード確認メッセージが表示される場合、「ダウンロード」ボタンをクリックする。

図 161 計算結果ファイルダウンロードダイアログ¶

3.ダウンロードした実行結果ファイルは圧縮されており、"out.zip"というファイル名になっている。: ファイルを解凍すると「ワークフローID名」のフォルダの下に「(ワークフローID+)ツール名」のフォルダが存在し、ツールの計算結果ファイルが格納されている( 図 162 )。

図 162 計算結果ファイル出力例¶