38. 多元系凝固計算/多元系凝固計算3Dワークフロー¶

38.1. 概要¶

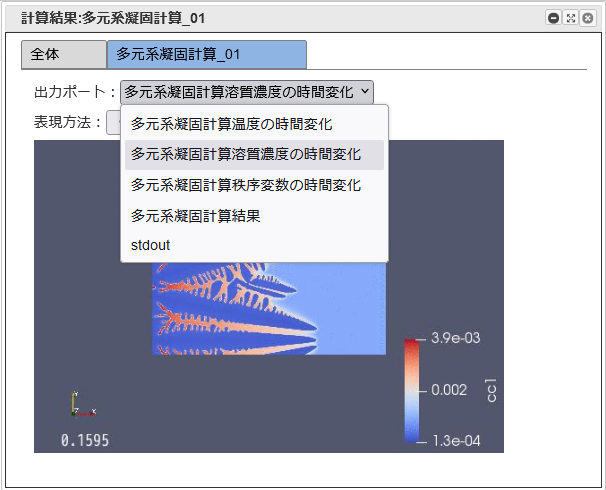
本ワークフローは多元系凝固モデルによる凝固組織のシミュレートを実装したワークフローであり、実行結果の表現方法によって、以下の2つに分けられている。

多元系凝固計算ワークフロー（2次元表現）
多元系凝固計算3Dワークフロー（3次元表現）

38.2. モデルの概要¶

本モデルは、N元系 \((N \geq2)\) の凝固組織をシミュレートするモデルであり、秩序変数 \(\phi (\phi =+1:固相、 \phi =-1:液相)\) 、元素 \(i\) の組成 \(c_i\) ( \(i = 1 \cdots N-1\) が溶質、\(i=N\) は溶媒)、温度 \(T\) の時間発展からなる。本モデルは定量的フェーズフィールド・モデル [Ref1] の中でも特に最新のモデル [Ref2] をベースに、計算コストを考慮して単純化したものである。また自由エネルギーや濃度場の取り扱いはKKSモデル [Ref3] やSteinbachらのグループのモデル [Ref4] と同様に"two-phase approach"に立脚しており、組成 \(c_i\) は固相の組成 \(c_{s,i}\) と液相の組成 \(c_{l,i}\) によって下記のように与えられる。

(1)¶\[c_i = \frac {1 + \phi}{2}c_{s,i} + \frac{1 - \phi}{2}c_{l,i}\]

また本モデルによる仮定と近似を以下に記す。

単相凝固のみを対象（共晶、包晶反応、その他の第二相の晶、析出はなし）
固相は立方晶系のみを対象
凝固収縮なし（固相と液相の密度は等しく、一定）
液相流動なし
固体の運動、変形なし
固液界面エネルギーは濃度・温度に依存しない
固液界面移動の駆動力は、温度と溶質組成に線形依存する（駆動力線形近似）
solute trappingなし（溶質分配の速度依存性無し）
温度場は外部入力（frozen temperature approximation）
拡散係数は温度に依存するが、組成には依存しない

38.2.1. \(\phi\) の方程式¶

秩序変数 \(\phi\) の時間発展方程式は下記のように与えられる。

(2)¶\[\begin{split}& \tau a_{s} (\mathbf{n})^{2} \frac {\partial \phi}{\partial \tau} = W^{2} \bigtriangledown \cdot \left [ a_{s} (\mathbf{n})^{2} \bigtriangledown \phi \right ] + W^{2} \sum_{r=x,y.z} \partial_{r} \left( | \bigtriangledown \phi |^{2} a_{s} (\mathbf{n}) \frac {\partial a_{s} (\mathbf{n})}{\partial ( \partial_{r} \phi )} \right) \\ & + \phi - \phi^{3} - ( 1 - \phi^{2} )^{2} a_{1} \frac {W}{\gamma} \Delta G_{driv}\end{split}\]

ここで、 \(W\) は界面幅[m]、 \(\gamma\) は界面エネルギー[ \(J/m^2\) ]、 \(a_{1}\) は定数( \(a_{1}\) =0.88388 )である。また、 \(\tau\) は

(3)¶\[\tau = a_{1} a_{2} \frac{W^{3}}{\gamma} \Delta S_{driv} \sum_{i=1}^{N-1} \frac{ ( 1 - k_{e,i} ) c_{l,i} m_{l,i} }{D_{l,i} }\]

と与えられ、\(a_{2}\) は定数( \(a_{2}\) = 0.62667 )、\(\Delta G_{driv}\) は変態のエントロピー[ \(J/m^3K\) ]、 \(k_{e,i}\) は溶質 \(i\) は溶質 \(i\) の液相線勾配[K/mole fraction]、 \(D_{l,i}\) は溶質 \(i\) の液相内拡散係数[ \(m^2/s\) ]である。 \(a_{s} (\mathbf{n})\) は固液界面の法線方向 \(\mathbf{n}\) に依存する関数であり、

(4)¶\[a_{s} (\mathbf{n}) = 1 - 3 \varepsilon_{4} + 4 \varepsilon_{4} \sum_{r=x,y,z} (\partial_{r} \phi)^{4} \left / \left( \sum_{r=x,y,z}(\partial_{r} \phi)^{2} \right)^2 \right.\]

と与えられる。ここで、 \(\varepsilon_{4}\) は固液界面エネルギーの異方性強度である。また、式 (2) の \(\Delta G_{driv}\) は固液界面移動の駆動力[ \(J/m^3\) ]であり、本モデルでは計算の高速化のため、下記のように近似している。

(5)¶\[\Delta G_{driv} = \Delta S_{driv} ( T - T_{0} ) + \Delta S_{driv} \sum^{N-1}_{i=1} m_{l,i} \left ( c_{l,i} - c^{e}_{l,i} \right )\]

ここで、 \(T_{0}\) は参照温度[K]、 \(c^{e}_{l,i}\) は \(T_{0}\) における溶質 \(i\) の液相線組成である。通常、 \(T_{0}\) は合金組成の液相線温度[K]、 \(c^{e}_{l,i}\) には合金組成を入力する。なお、 \(\Delta G_{driv}\) は、本来下記のように与えられる。

(6)¶\[\Delta G_{driv} = G_{s} ( T, \{ c_{s,i} \} ) - G_{l} ( T, \{ c_{l,i} \}) - \sum^{N-1}_{i} \Delta \mu_{c,i} (T, \{ c_{l,i} \} )(c_{s,i} - c_{l,i})\]

ここで、 \(G_{s}\) 、 \(G_{l}\) はそれぞれ固相と液相の自由エネルギー[ \(J/m^3\) ]、 \(\Delta \mu_{c,i}\) は溶質 \(i\) の拡散ポテンシャル[ \(J/m^3\) ]である。したがって、CALPHAD法から式 (6) の駆動力を予め求め、その温度依存性から式 (5) の \(\Delta S_{driv}\) を計算することができる。希薄固溶体の場合は、 \(\Delta S_{driv}\) = \(\Delta H / T_{m}\) と近似可能である。ここで、 \(\Delta H\) は単位体積あたりの凝固潜熱[ \(J/m^3\) ]、 \(T_{m}\) は純物質（溶媒）の融点[K]である。

38.2.2. 溶質 \(i\) の組成の時間発展¶

溶質 \(i\) の組成の時間発展は下記の方程式で記述される。

(7)¶\[\begin{split}& \left( \frac {1 + \phi}{2} k_{e,i} + \frac {1 - \phi}{2} \right) \partial_{t}c_{l,i} = \\ & \bigtriangledown \left( \left( k_{e,i} D_{s,i} \frac {1 + \phi}{2} + D_{l,i} \frac {1 - \phi}{2} \right) \bigtriangledown c_{l,i} + J_{at,i} + J_{noise,i} \right) + c_{l,i} ( 1 - k_{e,i} ) \frac { \partial_{t} \phi}{2}\end{split}\]

ここで、 \(J_{at,i}\) は

(8)¶\[J_{at,i} = - \frac {W}{2\sqrt{2}} \left( 1 - \frac {k_{e,i}D_{s,i}}{D_{l,i}} \right) c_{l,i} ( 1 - k_{e,i} ) \partial_{t} \phi \frac {\bigtriangledown \phi}{|\bigtriangledown \phi|}\]

と与えられる。また、 \(J_{noise,i}\) は熱揺らぎに起因する溶質拡散流束の揺らぎである。本モデルでは計算コストを低減するため、初期温度において \(D_{l,i}\) が最も大きい溶質 \(i=q\) にのみこの揺らぎを導入している。 \(J_{noise,i}\) は平均 \(\langle \Delta c \rangle\) の正規分布に従うノイズであり、その分散 \(\langle \sigma \rangle\) は

(9)¶\[\langle \sigma \rangle \propto \frac {1}{\Delta x^2 \Delta t} 2D_{l,q} c^{e}_{l,q} F_{u}\]

のように与えている。ここで、 \(\Delta x\) は空間グリッド間隔、 \(\Delta t\) は時間ステップ間隔、 \(F_{u}\) は定数であり、入力パラメータである。

38.2.3. 温度の時間発展¶

本モデルでは計算時間の短縮のために、熱伝導方程式を解く代わりに温度 \(T\) [K]の時間変化を以下の方程式で近似している。

(10)¶\[T = T_{initial} - C_{R} (t) \cdot t + G (X) \cdot X\]

ここで、 \(T_{initial}\) は初期温度[K]、 \(C_{R} (t)\) は冷却速度[K/s]、 \(G (X)\) は温度勾配[K/m]であり、 \(t\) は時間[s]、 \(X\) はx方向の空間座標[m]である。また、 \(C_{R} (t)\) はtの二次関数、 \(G (X)\) はXの二次関数として与えられる。

(11)¶\[C_{R} (t) = C_{R,0} + C_{R,1} \cdot t + C_{R,2} \cdot t^{2}\]

(12)¶\[G(X) = G_{0} + G_{1} \cdot X + G_{2} \cdot X^{2}\]

\(C_{R,0}\) 、 \(C_{R,1}\) 、 \(C_{R,2}\) および \(G_{0}\) 、 \(G_{1}\) 、 \(G_{2}\) は入力パラメータである。

38.3. 計算方法について¶

38.3.1. 差分法と安定条件¶

本モデルでは式 (2) と式 (7) を差分法によって解いている。いずれの方程式も空間方向には二次精度の差分を行い、時間方向は前進オイラー法で解いている。したがって、計算の安定条件を満足する必要があるため、時間ステップ \(\Delta t[s]\) を下記のように与える。

(13)¶\[\Delta t = \frac {\Delta x^2}{\alpha_{st}D_{l,q}}\]

ここで、\(D_{l,q}\) は初期温度における溶質 \(q\) の液相内拡散係数であり、溶質 \(q\) は前述の通り、最も大きな \(D_{l,i}\) の値を持つ溶質である。\(\alpha_{st}\) は定数であり、一次元計算では2以上、二次元計算では4以上、三次元計算では6以上の値に設定する。式 (13) は計算の安定条件が溶質の拡散方程式で決まることを想定したものであり、一般の凝固条件であれば、この形で安定に計算可能である。ただし凝固条件によっては、拡散方程式ではなく \(\phi\) の方程式の安定条件を成立させる必要があり、その場合は \(\alpha_{st}\) の値を大きすることでその安定条件を満足させる必要がある。

38.3.2. 境界条件¶

本モデルでは、\(\phi\) と \(c_i\) に対して、x,y,z方向のそれぞれに対して異なる境界条件を設定できる。境界条件の種類は、: 1) ゼロノイマン条件

2) 鏡面対称条件

3) 周期的境界条件

から選択する。その設定は入力ファイルで行う。なお一次元計算ではyとz方向をゼロノイマン条件、二次元計算ではz方向をゼロノイマン条件に設定する必要がある。

38.3.3. 初期状態の設定¶

本モデルでは核生成は扱わず、初期に固相が存在している状況から計算をスタートする。初期状態として、まず、: 1) 合金組成

2) 初期温度
を設定する。さらに、固相の: 3) 形態（球形・円形、もしくは板状）

4) 初期サイズ（球形・円形の場合は半径、板状の場合は厚さ）

5) 個数（球形・円形の場合のみ。板状は1つのみ）

6) 位置（球形・円形の場合のみ。メッシュ座標で指定）

7) オイラー角（z-y-z系の三つの角度）

を設定する。固相の形態が板状のとき、厚さ方向はx方向で、その数は1つのみ。なお、リスタート計算を選択した場合には2)〜7)の情報は無視され、restart.outの情報から再計算がスタートする。

38.4. 多元系凝固計算ワークフロー（2次元表現）¶

多元系凝固計算ワークフローで使用されるツールの説明とサンプル入出力ファイルを示す。

38.4.1. 多元系凝固計算¶

図 796 多元系凝固計算¶

入力ファイル：

ポート名：多元系凝固計算パラメータ
メッシュサイズ、cudaのスレッド数、境界条件、合金物性値、凝固条件、結果の出力条件、組織の初期状態等の全ての設定を行う。
設定方法を以下に示す。

input file
- - - - im    jm    km-
    2048   1024   1
- - - - threadx thready threadz-
    16   16   1
- - - - system size [m]
    6e-4
- - - - boundary condition for x, y, z (0:Neumann, 1:Mirror, 2:Periodic)
    2 2 0
- - - - total number of time steps
    100000
- - - - constant related to time step
    5.0
- - - - restart (0=usual start, 1 = restart)
    0
- - - - initial temperature [K]
    1800
- - - - cooling rate [K/s] Cr = Cr0 + Cr1*t + Cr2*t^2
    20.0 0.0 0.0
- - - - temperature gradient [K/m] G = G0 + G1*x + G2*x^2
    0 0.0 0.0
- - - - interfacial energy [J/m2] and anisotropy strength
    0.2    0.02
- - - - reference temperature
    1802.5
- - - - transformation entropy per volume [J/m3K]
    1.0e+6
- - - - number of solute elements
    2
- - - - liquidus slope [K/mol frac], partition coef, initial comp.
- - - - prefactor and activation energy of L and S diffusivities
    1666.7 0.17 0.003
    5.2e-7 48957.88 1.27e-6 81387.24
    490 0.74 0.007
    3.85e-7 69461.6 7.6e-5 224453
- - - - WW / dx
    1.3
- - - - threshold value of phi
    1e-6
- - - - on-off switch of antitrapping current
    1.0
- - - - noise amplitude, mean and standard deviation
    1e-22   0.0
- - - - integers for output files
    10000  2 2 1
- - - - restart file (0=ignore, 1=output)
    0
- - - - solid_shape ( 1 = spherical or circle, 2 = plate)
    1
- - - - number of initial grains
    5
- - - - initial radius of grains [m]
    1e-6
- - - - position, Euler angle
    256 768 1  15.0 0.0 0.0
    1296 648 1  -30.0 0.0 0.0
    1560 80 1  45.0 0.0 0.0
    600 360 1  2.0 0.0 0.0
    1800 400 1  28.0 0.0 0.0

各項目の説明：

im jm km

2048 1024 1 : x,y,z方向のメッシュ数

threadx, thready, threadz

16 16 1 : GPU並列計算におけるx,y,z方向のスレッド数

system size[m]

6e-4 : x方向のシステムサイズ（これをx方向のメッシュ数で割ったものが \(\Delta x\) ）

boundary condition for x,y,z(0:Neumann, 1:Mirror, 2:Preiodic)

2 2 0 : x,y,z方向の境界条件の指定（全ての変数）。0はゼロノイマン条件、1は鏡面対称条件、2は周期的境界条件。メッシュ数が1の方向は必ず0に設定。

total number of time steps

100000 : 時間ステップ数。計算でシミュレートする時間をステップ数で指定する。必要な時間を8.6590583896379987E-007で割り算する。

constant related to time step

5.0 : 式 (13) の \(\alpha_{st}\)

restart(0=usual start, 1=restart)

0 : 0 のときはこの入力ファイルの初期状態を読み込んで計算がスタート。1 のときは、前回の計算の出力ファイルrestart.outから \(\phi\) 、{\(C_{l,i}\)}、{\(T\)} とオイラー角の情報を読み込んで、再計算がスタート。

initial temperature [K]

1800 : 初期温度、 \(T_{initial}\) [K]

cooling rate [K/s]

20.0 0.0 0.0 : 冷却速度。左から、式 (11) の \(C_{R,0}\)、\(C_{R,1}\)、\(C_{R,2}\) の値。

temperature gradient [K/m]

0 0.0 0.0 : 温度勾配。左から、式 (12) の \(G_0\)、\(G_1\)、\(G_2\) の値。

interfacial energy [J/m2] and anisotropy strength

0.2 0.02 : 固液界面エネルギー \({\gamma[J/m^2]}\) と異方性強度 \(\varepsilon_4\)

reference temperature

1802.5 : 参照温度 \(T_0[K]\)

transformation entropy per volume [J/m3K]

1.0e+6 : 変態のエントロピー \(\Delta S_{driv}[J/m^3K]\)

number of solute elements

2 : 溶質元素の数

liquidus slope [K/mol frac], partition coef, initial comp
prefactor and activation energy of L and S diffusivities

1666.7 0.17 0.003 : 溶質1の液相線勾配 \(m_{l,i}\)、初期組成 \(c_i\)

5.2e-7 48957.88 1.27e-6 81387.24 : 溶質1の \(D_{l,i}^0\)、\(Q_{l,i}\)、\(D_{s,i}^0\)、\(Q_{s,i}\) 。ここで、液相内拡散係数は \(D_{l,i} = D_{l,i}^0\exp(-Q_{l,i}/RT)\) と与えられ、固相内拡散係数は \(D_{s,i} = D_{s,i}^0\exp(-Q_{s,i}/RT)\) と与えられる。

490 0.74 0.007 : 溶質２の液相線勾配 \(m_{l,i}\)、初期組成 \(c_i\)

3.85e-7 69461.6 7.6e-5 224453 : 溶質２の \(D_{l,i}^0\)、\(Q_{l,i}\)、\(D_{s,i}^0\)、\(Q_{s,i}\) 。ここで、液相内拡散係数は \(D_{l,i} = D_{l,i}^0\exp(-Q_{l,i}/RT)\) と与えられ、固相内拡散係数は \(D_{s,i} = D_{s,i}^0\exp(-Q_{s,i}/RT)\) と与えられる。

WW / dx

1.3 : 界面厚さを指定する変数であり、式 (2) の \(W\) を \(W = \alpha_w\Delta x\) と与えた時の \(\alpha_w\) の値。通常は1～2の範囲。精度と計算コストのバランスから1.2～1.5くらいが推奨値。

threshold value of phi

1e-6 : \(\phi\) の閾値 \(\phi_c\)。\(-1+\phi_c ≦ \phi ≦ 1 - \phi_c\) の領域のみで \(\phi\) の時間変化を計算。1e-6 以下を推奨。

on-off switch of antitrapping current

1.0 : 0のときは式 (8) の流束を無視。1のときは考慮。通常は1に設定。

noise amplitude, mean and standard deviation

1e-22 0.0 : 式 (9) におけるFuの値と、\(J_{noise,i}\) の平均 \(\langle \Delta_c \rangle\)

integers for output files

10000 2 2 1：VTKファイルを出力する時間ステップ間隔（この例では10000回に1回VTKファイルを出力）と、VTKファイルにおけるx, y, z方向のデータ・スキップ数。

restart file (0=ignore, 1=output)

1：0のとき、リスタートファイル(restart.out)を出力しない。1のとき出力する。

solid_shape ( 1 = spherical or circle, 2 = plate)

1 ：初期の固相の形状。1は球形、または円形、2は板状

number of initial grains

5：初期の固相粒子の数。形状が板状のときには、この値は無視され、固相は一つのみ設置される。

initial radius of grains [m]

1e-6：初期の固相サイズ[m]。球形・円形のときにはその半径を表す。

position, Euler angle

256 768 1 15.0 0.0 0.0：初期の固相粒子の中心座標(i, j, k)とオイラー角（z-yz-系）。i, j, kはメッシュ座標。粒子の個数分だけ行を変えて記入。板状のときは一行目の情報のみが読み込まれる。

出力ファイル：

当ツールはパラメータファイルの時間ステップ数ごとにすべての状態変数（秩序変数 \(\phi\)、全ての溶質の組成{ \(c_i\) }、温度 \(T\) [K]）を計算結果として保存する。保存されたそれぞれの状態変数を取り出して画像化し、アニメーション（進展画像、フォーマットはGIF）を出力している。

ポート名：多元系凝固計算温度の時間変化
温度の状態変数を画像化し、まとめてアニメーション化したもの( 図 797 )。

図 797 出力ファイル「多元系凝固計算温度の時間変化」¶

ポート名：多元系凝固計算溶質濃度の時間変化

溶質の組成状態変数を画像化し、まとめてアニメーション化したもの( 図 798 )。

図 798 出力ファイル「多元系凝固計算溶質濃度の時間変化」¶

ポート名：多元系凝固計算秩序変数の時間変化

秩序変数 \(\phi\) の状態を画像化し、まとめてアニメーション化したもの( 図 799 )。

図 799 出力ファイル「多元系凝固計算秩序変数の時間変化」¶

ポート名：多元系凝固計算結果

計算の結果、出力されたVTKファイルをZIPファイルにまとめたもの( 図 800 )。

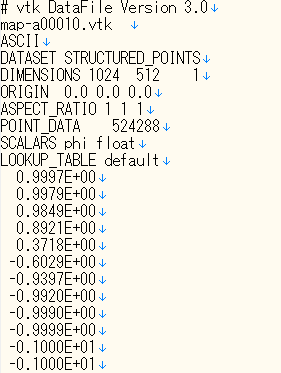
../_images/solidmulti_workflow_result_vtk.png

図 800 出力ファイル「多元系凝固計算結果」内のVTKファイル¶

38.4.2. サンプル入出力ファイル¶

入力ファイルの多元系凝固計算パラメータの例と対応する計算結果例を示す。

サンプル1:Fe-C-Mn合金の等軸デンドライト成長の2D計算

サンプル入出力ファイル1 ダウンロードはこちら （html版のみダウンロード可能）
- 予測モジュール提供元から受領した入力ファイルにて検証済

多元系凝固計算パラメータ

input file
- - - - im    jm    km-
    2048   1024   1
- - - - threadx thready threadz-
    16   16   1
- - - - system size [m]
    6e-4
- - - - boundary condition for x, y, z (0:Neumann, 1:Mirror, 2:Periodic)
    2 2 0
- - - - total number of time steps
    100000
- - - - constant related to time step
    5.0
- - - - restart (0=usual start, 1 = restart)
    0
- - - - initial temperature [K]
    1800
- - - - cooling rate [K/s] Cr = Cr0 + Cr1*t + Cr2*t^2
    20.0 0.0 0.0
- - - - temperature gradient [K/m] G = G0 + G1*x + G2*x^2
    0 0.0 0.0
- - - - interfacial energy [J/m2] and anisotropy strength
    0.2   0.02
- - - - reference temperature
    1802.5
- - - - transformation entropy per volume [J/m3K]
    1.0e+6
- - - - number of solute elements
    2
- - - - liquidus slope [K/mol frac], partition coef, initial comp.
- - - - prefactor and activation energy of L and S diffusivities
    1666.7 0.17 0.003
    5.2e-7 48957.88 1.27e-6 81387.24
    490 0.74 0.007
    3.85e-7 69461.6 7.6e-5 224453
- - - - WW / dx
    1.3
- - - - threshold value of phi
    1e-6
- - - - on-off switch of antitrapping current
    1.0
- - - - noise amplitude, mean and standard deviation
    1e-22  0.0
- - - - integers for output files
    10000 2 2 1
- - - - restart file (0=ignore, 1=output)
    0
- - - - solid_shape ( 1 = spherical or circle, 2 = plate)
    1
- - - - number of initial grains
    5
- - - - initial radius of grains [m]
    1e-6
- - - - position, Euler angle
    256 768 1  15.0 0.0 0.0
    1296 648 1  -30.0 0.0 0.0
    1560 80 1  45.0 0.0 0.0
    600 360 1  2.0 0.0 0.0
    1800 400 1  28.0 0.0 0.0

出力結果は、図 797 、図 798 、図 799 となる。

サンプル2:Al-Si-Cu合金の一方向凝固の2D計算

サンプル入出力ファイル2 ダウンロードはこちら （html版のみダウンロード可能）
- 予測モジュール提供元から受領した入力ファイルにて検証済

多元系凝固計算パラメータ

input file
- - - - im    jm    km-
    2048   1024   1
- - - - threadx thready threadz-
    16   16   1
- - - - system size [m]
    4e-4
- - - - boundary condition for x, y, z (0:Neumann, 1:Mirror, 2:Periodic)
    0 2 0
- - - - total number of time steps
    1e5
- - - - constant related to time step
    5.0
- - - - restart (0=usual start, 1 = restart)
    0
- - - - initial temperature [K]
    930
- - - - cooling rate [K/s] Cr = Cr0 + Cr1*t + Cr2*t^2
    20.0 0.0 0.0
- - - - temperature gradient [K/m] G = G0 + G1*x + G2*x^2
    10000 0.0 0.0
- - - - interfacial energy [J/m2] and anisotropy strength
    0.2   0.02
- - - - reference temperature
    931.63
- - - - transformation entropy per volume [J/m3K]
    1.0e+6
- - - - number of solute elements
    2
- - - - liquidus slope [K/mol frac], partition coef, initial comp.
- - - - prefactor and activation energy of L and S diffusivities
    600 0.13 1e-3
    1.34e-7 30000 1.38e-5 1.18e5
    620 0.14 2e-3
    1.06e-7 2.4e4 4.44e-5 1.34e5
- - - - WW / dx
    1.3
- - - - threshold value of phi
    1e-6
- - - - on-off switch of antitrapping current
    1.0
- - - - noise amplitude, mean and standard deviation
    1e-22  0.0
- - - - integers for output files
    1e4   2 2 1
- - - - restart file (0=ignore, 1=output)
    0
- - - - solid_shape ( 1 = spherical or circle, 2 = plate)
    1
- - - - number of initial grains
    3
- - - - initial radius of grains [m]
    1e-6
- - - - position, Euler angle
    1 128 1  0.0 0.0 0.0
    1 512 1  -10.0 0.0 0.0
    1 670 1  15.0 0.0 0.0

図 801 最終タイムステップ時におけるCuの濃度マップ¶

38.5. 多元系凝固計算3Dワークフロー（3次元表現）¶

多元系凝固計算3Dワークフローで使用されるツールの説明とサンプル入出力ファイルを示す。

38.5.1. 多元系凝固計算3D¶

図 802 多元系凝固計算3D¶

入力ファイル：

ポート名：多元系凝固計算パラメータ
メッシュサイズ、cudaのスレッド数、境界条件、合金物性値、凝固条件、結果の出力条件、組織の初期状態等の全ての設定を行う。
各項目の説明は、 多元系凝固計算ワークフロー（2次元表現） の多元系凝固計算パラメータの説明を参照。

出力ファイル：

当ツールはパラメータファイルの時間ステップ数ごとにすべての状態変数（秩序変数 \(\phi\)、全ての溶質の組成{ \(c_i\) }、温度 \(T\) [K]）を計算結果として保存する。保存されたそれぞれの状態変数を取り出して画像化し、アニメーション（進展画像、フォーマットはGIF）を出力している。

ポート名：多元系凝固計算温度の時間変化
温度の状態変数を画像化し、まとめてアニメーション化したもの( 図 803 )。

../_images/solidmulti_workflow_3d_temp.jpg

図 803 出力ファイル「多元系凝固計算温度の時間変化」¶

ポート名：多元系凝固計算溶質濃度の時間変化

溶質の組成状態変数を画像化し、まとめてアニメーション化したもの( 図 804 )。

../_images/solidmulti_workflow_3d_cc1.jpg

図 804 出力ファイル「多元系凝固計算溶質濃度の時間変化」¶

ポート名：多元系凝固計算秩序変数の時間変化

秩序変数 \(\phi\) の状態を画像化し、まとめてアニメーション化したもの( 図 805 )。

../_images/solidmulti_workflow_3d_phi.jpg

図 805 出力ファイル「多元系凝固計算秩序変数の時間変化」¶

ポート名：多元系凝固計算結果

計算の結果、出力されたVTKファイルをZIPファイルにまとめたもの( 図 806 )。

../_images/solidmulti_workflow_3d_result_vtk.png

図 806 出力ファイル「多元系凝固計算結果」内のVTKファイル¶

38.5.2. サンプル入出力ファイル¶

入力ファイルの多元系凝固計算パラメータの例と対応する計算結果例を示す。

サンプル3:Fe-C合金の等温凝固の3D計算

サンプル入出力ファイル3 ダウンロードはこちら （html版のみダウンロード可能）
- 予測モジュール提供元から受領した入力ファイルにて検証済

多元系凝固計算パラメータ

input file
- - - - im    jm    km-
512   768  256
- - - - threadx thready threadz-
16   16   1
- - - - system size [m]
8e-5
- - - - boundary condition for x, y, z (0:Neumann, 1:Mirror, 2:Periodic)
2 1 1
- - - - total number of time steps
40000
- - - - constant related to time step
7.0
- - - - restart (0=usual start, 1 = restart)
0
- - - - initial temperature [K]
1800
- - - - cooling rate [K/s] Cr = Cr0 + Cr1*t + Cr2*t^2
0.0 0.0 0.0
- - - - temperature gradient [K/m] G = G0 + G1*x + G2*x^2
0 0.0 0.0
- - - - interfacial energy [J/m2] and anisotropy strength
0.2       0.02
- - - - reference temperature
1802.5
- - - - transformation entropy per volume [J/m3K]
1.0e+6
- - - - number of solute elements
1
- - - - liquidus slope [K/mol frac], partition coef, initial comp.
- - - - prefactor and activation energy of L and S diffusivities
1666.7 0.17 0.003
5.2e-7 48957.88 1.27e-6 81387.24
- - - - WW / dx
1.3
- - - - threshold value of phi
1e-7
- - - - on-off switch of antitrapping current
1.0
- - - - noise amplitude, mean and standard deviation
0e-22      0.0
- - - - integers for output files
4000      2 2 2
- - - - restart file (0=ignore, 1=output)
0
- - - - solid_shape ( 1 = spherical or circle, 2 = plate)
1
- - - - number of initial grains
1
- - - - initial radius of grains [m]
1e-6
- - - - position, Euler angle
256 1 1  0.0 0.0 0.0

出力結果は、図 803 、図 804 、図 805 となる。

38.6. ワークフローの実行¶

38.6.1. ワークフローの選択¶

ワークフロー一覧画面で対象のワークフローのリンクをクリックする。

図 807 ワークフロー選択画面¶

38.6.2. 実行選択¶

ワークフローメタ情報画面で、「ワークフローを実行」ボタンをクリックする。このときワークフローのステータスが「公開中」であることを確認する。( 図 808 )

../_images/solidmulti_workflow_overview.png

図 808 実行開始¶

38.6.3. パラメータ入力と実行¶

入力ファイルをアップロードする。「参照」を選択後、「参照」ボタンをクリックして入力ファイルを指定する。

必要に応じて、「実行」ボタンクリック前に「ラン説明」にランに関する詳細説明を入力する。

入力ファイルアップロード後、「実行」ボタンをクリックする。( 図 809 )

../_images/solidmulti_workflow_execute.png

図 809 パラメータ入力と実行¶

38.7. 計算結果の確認¶

38.7.1. ダウンロード¶

計算が終了すると、計算結果をダウンロードすることが可能になる。

ラン一覧画面からステータスが「完了」のランを選択し、ラン詳細画面を表示する。ラン詳細画面の「ダウンロード」ボタンをクリックする（図 810 ）と、計算結果ファイルダウンロード画面に遷移する。

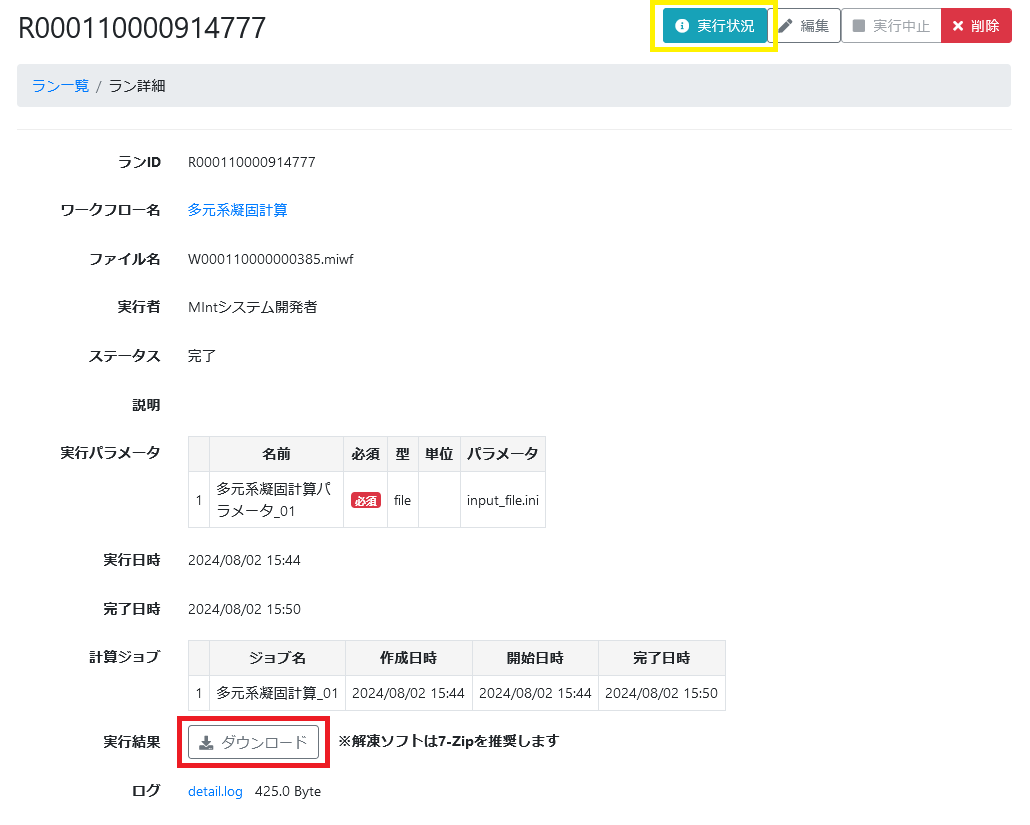
../_images/solidmulti_workflow_results.png

図 810 計算結果のダウンロード¶

ダウンロードファイルを解凍すると「ワークフローID名」のフォルダの下に「(ワークフローID+)ツール名」のフォルダが存在し、ツールの結果ファイルが格納されている。

38.7.2. 画像の確認¶

モジュールによっては出力ファイルの画像での確認が可能なものがある。当ワークフローも計算結果をいくつかの画像ファイルで出力している。計算結果の確認の「ラン一覧」から該当ランを選択し、図 810 の黄枠の「実行状況」を押下することで閲覧可能となる。

参照したいモジュールを押下し、メニューから電卓アイコンを押下する( 図 811 )

../_images/solidmulti_workflow_result_view01.png

図 811 計算結果の表示¶

表示されたダイアログの出力ポート選択肢（コンボボックス）の選択肢をいくつか選択すると内容に応じた表示が行われる。

../_images/solidmulti_workflow_result_view02.png

図 812 画像の表示例¶

Ref1

Karma, Phys. Rev. Lett., 87 (2001), 115701.

Ref2

Ohno, T. Takaki and Y. Shibuta, Phys. Rev. E, 96 (2017), 033311.

Ref3

1. Kim, W. T. Kim, and T. Suzuki, Phys. Rev. E, 60 (1999), 7186.

Ref4

Tiaden, B. Nestler, H.J. Diepers, I. Steinbach, Physica D, 115 (1998), 73.

38. 多元系凝固計算/多元系凝固計算3Dワークフロー¶

38.1. 概要¶

38.2. モデルの概要¶

38.2.1. \(\phi\) の方程式¶

38.2.2. 溶質 \(i\) の組成の時間発展¶

38.2.3. 温度の時間発展¶

38.3. 計算方法について¶

38.3.1. 差分法と安定条件¶

38.3.2. 境界条件¶

38.3.3. 初期状態の設定¶

38.4. 多元系凝固計算ワークフロー（2次元表現）¶

38.4.1. 多元系凝固計算¶

38.4.2. サンプル入出力ファイル¶

38.5. 多元系凝固計算3Dワークフロー（3次元表現）¶

38.5.1. 多元系凝固計算3D¶

38.5.2. サンプル入出力ファイル¶

38.6. ワークフローの実行¶

38.6.1. ワークフローの選択¶

38.6.2. 実行選択¶

38.6.3. パラメータ入力と実行¶

38.7. 計算結果の確認¶

38.7.1. ダウンロード¶

38.7.2. 画像の確認¶

目次

前のトピックへ

次のトピックへ